|
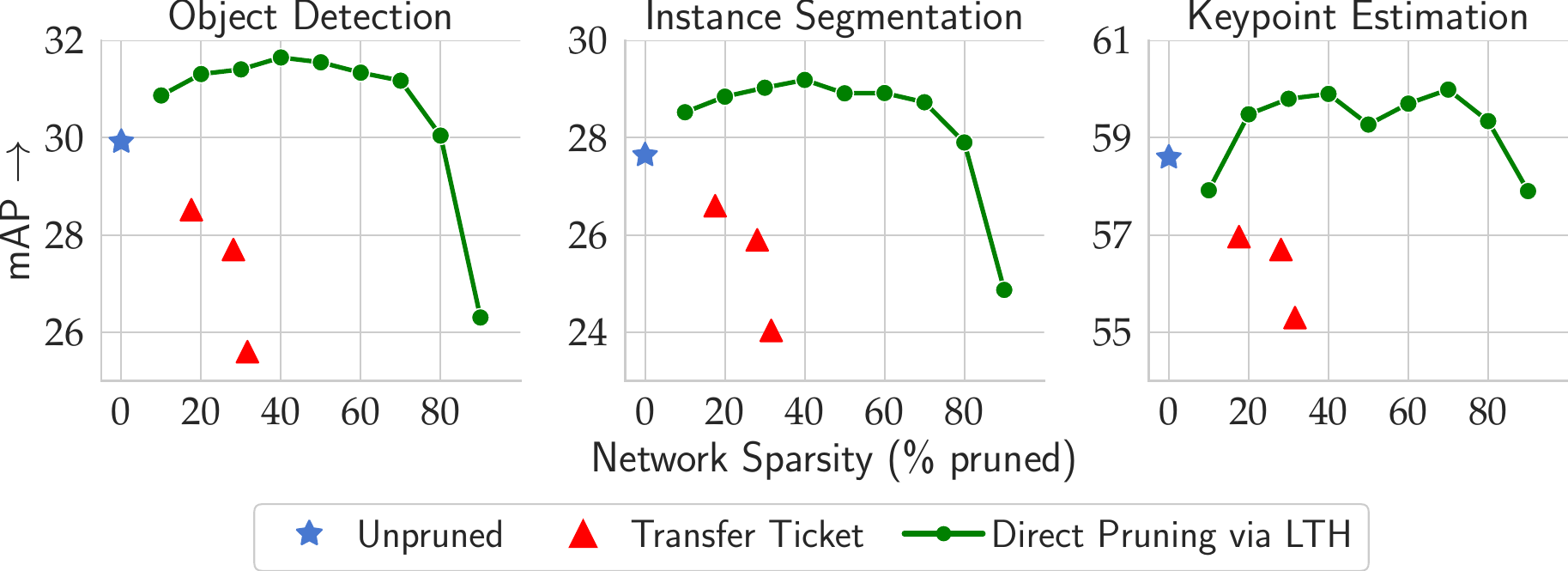
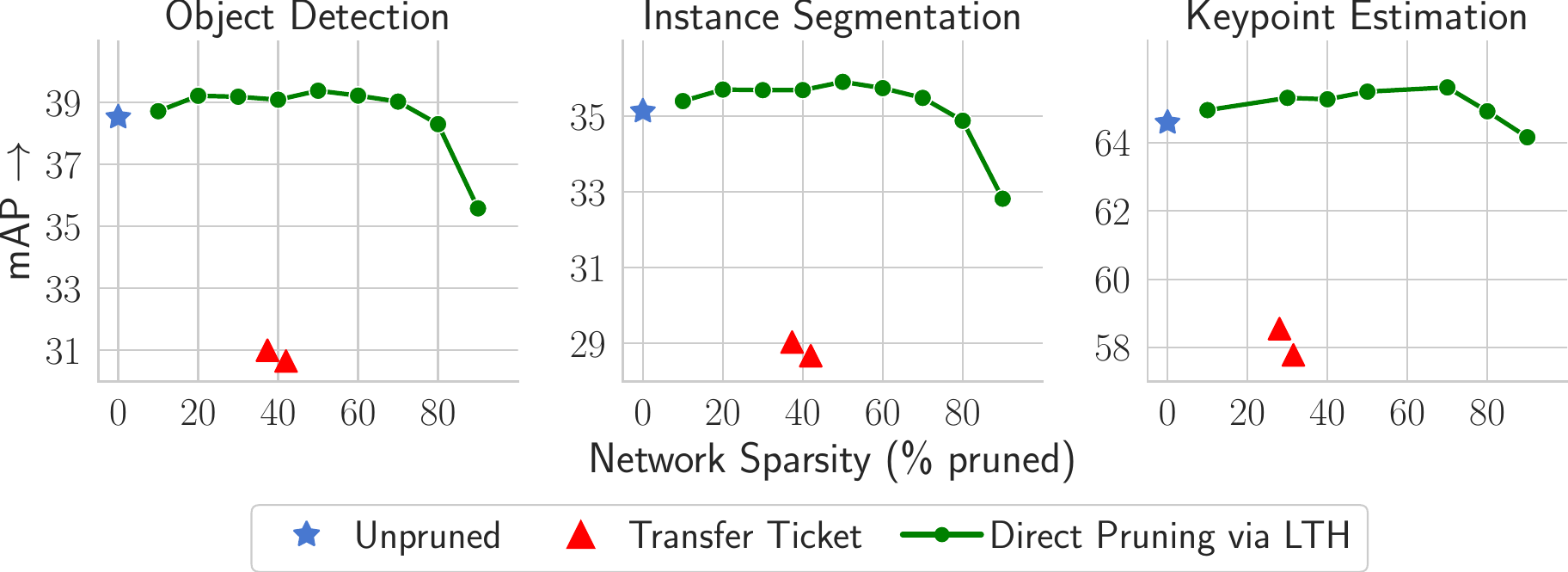
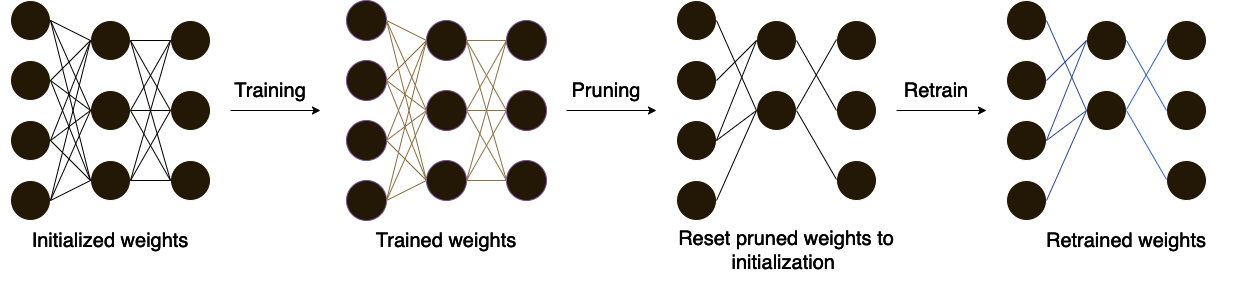
Recognition tasks, such as object recognition and keypoint estimation, have seen widespread adoption in recent years. Most state-of-the-art methods for these tasks use deep networks that are computationally expensive and have huge memory footprints. This makes it exceedingly difficult to deploy these systems on low power embedded devices. Hence, the importance of decreasing the storage requirements and the amount of computation in such models is paramount. The recently proposed Lottery Ticket Hypothesis (LTH) states that deep neural networks trained on large datasets contain smaller subnetworks that achieve on par performance as the dense networks. In this work, we perform the first empirical study investigating LTH for model pruning in the context of object detection, instance segmentation, and keypoint estimation. Our studies reveal that lottery tickets obtained from ImageNet pretraining do not transfer well to the downstream tasks. We provide guidance on how to find lottery tickets with up to 80% overall sparsity on different sub-tasks without incurring any drop in the performance. Finally, we analyse the behavior of trained tickets with respect to various task attributes such as object size, frequency, and difficulty of detection.
|